Pflichtteil 2013 - Aufgabe 8
Neun Spielkarten (vier Asse, drei Könige und zwei Damen) liegen verdeckt auf dem Tisch.
a) ... (ist für unser Thema "Zufallsvariablen und Erwartungswert" nicht relevant)
b) Die neun Spielkarten werden gemischt und erneut verdeckt ausgelegt.
Laura dreht nun so lange Karten um und lässt sie aufgedeckt auf dem Tisch liegen,
bis ein Ass erscheint. Die Zufallsvariable X gibt die Anzahl der aufgedeckten Spielkarten an.
Welche Werte kann X annehmen?
Berechnen Sie P(X≤2).
(4 VP)
Lösung zu b)Es gibt insgesamt 9 Karten. Ein Ass wird frühestens beim ersten und spätestens beim sechsten Umdrehen aufgedeckt, daher kann X nur Werte zwischen 1 und 6 annehmen. Es gilt
P(X=1) = 4/9, P(X=2) = 5/9 · 4/8 = 5/18
und somitP(X≤2) = P(X=1) + P(X=2) = 4/9 + 5/18 = 13/18 ≈ 72,2%.
Ergebnis: X ∈ {1,2,3,4,5,6} und P(X≤2) = 13/18 ≈ 72,2%.Pflichtteil 2016 - Aufgabe 8:
Bei einem Glücksrad werden die Zahlen 1, 2, 3 und 4 bei einmaligem Drehen mit folgenden Wahrscheinlichkeiten angezeigt:
| Zahl | 1 | 2 | 3 | 4 |
| Wahrscheinlichkeit | 0,4 | 0,1 | 0,3 | 0,2 |
a) ... (ist für unser Thema "Zufallsvariablen und Erwartungswert" nicht relevant)
b) An dem Glücksrad sollen nur die Wahrscheinlichkeiten für die Zahlen 1 und 2 so verändert werden, dass das folgende Spiel fair ist:
Für einen Einsatz von 2,50 € darf man einmal am Glücksrad drehen.
Die angezeigte Zahl gibt den Auszahlungsbetrag in Euro an.
Bestimmen Sie die entsprechenden Wahrscheinlichkeiten für die Zahlen 1 und 2.
(4 VP)
LösungWir modellieren den Auszahlungsbetrag als Zufallsvariable X. Laut Aufgabenstellung kann X die Werte 1, 2, 3 oder 4 (Euro) annehmen. Wenn das Spiel fair sein soll, muss der erwartete Auszahlungsbetrag dem Einsatz entsprechen. Es muss also E(X)=2,5 gelten. Die neuen Wahrscheinlichkeiten für die Zahlen 1 und 2 seien a und b. Es folgt
E(X) = a·1 + b·2 + 0,3·3 + 0,2·4 = 2,5
⇔ a·1 + b·2 + 1,7 = 2,5
⇔ a + 2b = 0,8
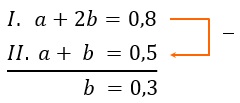
Ergebnis:
Damit das Spiel fair wird, müssen die Wahrscheinlichkeiten (und damit das Glücksrad) so verändert werden, dass die 1 mit einer Wahrscheinlichkeit von 0,2 (20 %) und die 2 mit einer Wahrscheinlichkeit von 0,3 (30 %) gedreht wird.
Aufgabe B 2.2
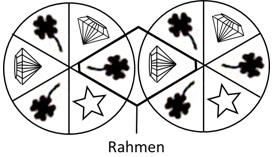
Auf zwei Glücksrädern befinden sich jeweils sechs gleich große Felder. Bei jedem Spiel werden die Räder einmal in Drehung versetzt. Sie laufen dann unabhängig voneinander aus und bleiben so stehen, dass von jedem Rad genau ein Feld im Rahmen sichtbar ist.
a) Zunächst werden die Räder als ideal angenommen.
Bei einem Einsatz von 0,20 € sind folgende Auszahlungen vorgesehen:
Stern - Stern 2,00 €
Diamant - Diamant 0,85 €
Kleeblatt - Kleeblatt 0,20 €
In allen anderen Fällen wird nichts ausbezahlt.
Weisen Sie nach, dass das Spiel fair ist.
Nun möchte der Veranstalter auf lange Sicht pro Spiel 5 Cent Gewinn erzielen. Dazu soll nur der Auszahlungsbetrag für "Diamant - Diamant" geändert werden. Berechnen Sie diesen neuen Auszahlungsbetrag.
(3 VP)
Lösung a)Nachweis, dass das Spiel fair ist
Es seien K = Kleeblatt, S = Stern und D = Diamant.
Die Wahrscheinlichkeiten für ein einzelnes Glücksrad sind:
P(K)=3/6, P(S)=1/6, P(D)=2/6
Bei zwei identischen Glücksrädern und unabhängigen Drehungen gilt dann:P(S,S) = 1/6 · 1/6 = 1/36, P(D,D) = 2/6 · 2/6 = 4/36, P(K,K) = 3/6 · 3/6 = 9/36
undP(alle anderen Kombinationen) = 1 - (1/36 + 4/36 + 9/36) = 22/36.
Die Zufallsvariable X steht nachfolgend für die verschiedenen möglichen Gewinne. Somit kann X die Werte 2; 0,85; 0,2 oder 0 annehmen. Es folgt
P(X=2) = P(S,S) = 1/36,
P(X=0,85) = P(D,D) = 4/36,
P(X=0,2) = P(K,K) = 9/36 und
P(X=0) = P(andere) = 22/36
E(X)=2·P(X=2) + 0,85·P(X=0,85) + 0,2·P(X=0,2) + 0·P(X=0)
= 2·1/36 + 0,85·4/36 + 0,2·9/36 + 0 = 0,2
Ergebnis: Auf lange Sicht kann man einen Gewinn von 20 Cent pro Spiel erwarten. Dies entspricht aber genau dem Einsatz, d.h. das Spiel ist fair!
Neuer Auszahlungsbetrag für "Diamant - Diamant"
Der Veranstalter möchte auf lange Sicht 5 Cent pro Spiel gewinnen. Da der Einsatz nach wie vor 0,20 € beträgt, muss nun der Erwartungswert, also der erwartete Gewinn pro Spiel, auf 0,15 € zurückgesetzt werden. Wir setzen, wie verlangt, den Gewinn für "Diamant-Diamant" neu an und nennen diesen a. Damit gilt:
E(X) = 2·P(X=2) + a·P(X=a) + 0,2·P(X=0,2)
= 2·1/36 + a·4/36 + 0,2·9/36 = 0,15
Ergebnis: Der neue Auszahlbetrag für "Diamant-Diamant" liegt bei 0,40 €.
| Downloads |
PowerPoint